Тема 5.Коло та круг.

 Коло, описане навколо трикутника.

Означення. Коло називають описаним навколо трикутника, якщо воно проходить через усі його вершини.

Теорема. Навколо будь-якого трикутника можна описати коло.

Властивості

Для кращого сприйняття означення кола, описаного навколо трикутника, та його властивості варто скористатись малюнком “Описане коло”. Так ви зможете наочно побачити відповідне коло та його властивості.

Описане коло

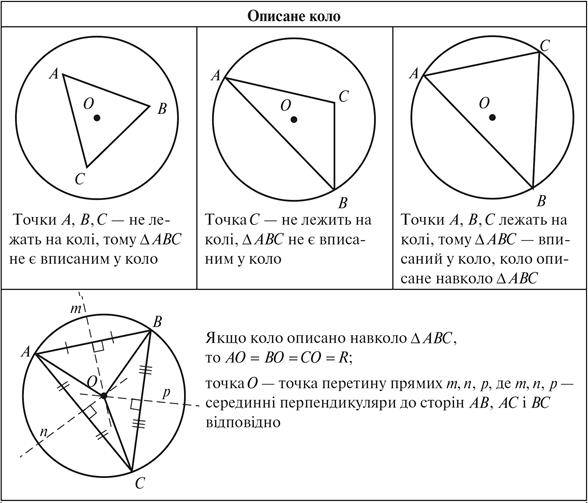
Випадки розташування центра кола:

• описаного навколо гострокутного трикутника міститься всередині трикутника;
• описаного навколо прямокутного трикутника – на середині гіпотенузи.
• описаного навколо тупокутного трикутника – поза трикутником;

Взаємне розміщення двох кіл.

Дотична до кола.

На площині пряма і коло можуть перетинатися або не перетинатися. При перетині вони можуть мати одну або дві спільні точки.

1. Якщо відстань від центра кола до прямої більша від радіуса, то в прямої і кола немає спільних точок.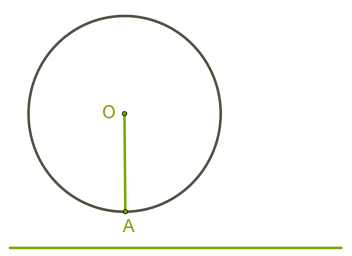

 

 

2. Якщо відстань від центра кола до прямої менша від радіуса, то в прямої і кола дві спільні точки.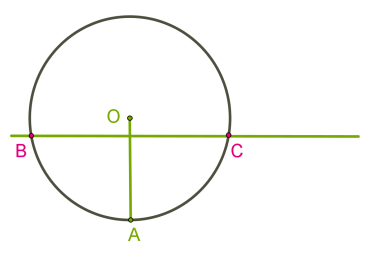

 

 

У цьому випадку пряму називають січною кола.

Якщо пряма має дві спільні точки з колом, то вона називається січною.

3. Якщо відстань від центра кола до прямої дорівнює радіусу, то в прямої і кола одна спільна точка.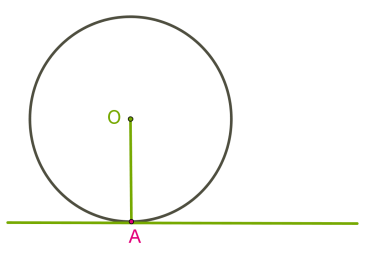

 

 

У цьому випадку пряму називають дотичною до кола.

Дотичною до кола називається пряма, що має з колом одну спільну точку.

Дотична до кола перпендикулярна радіусу, проведеному до точки дотику.

 

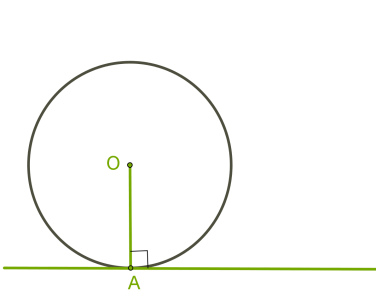Припустимо, що радіус OA не перпендикулярний до прямої, але є похилим. Тоді з точки O можна провести перпендикуляр до прямої, який буде коротшим, ніж радіус.

 

Це означає, що відстань від центра кола до прямої менша від радіуса, і в прямої та кола повинні бути дві спільні точки. Але це суперечить умові, тож наше припущення неправильне.

Якщо з точки до кола проведено дві дотичні, то:
a) довжини відрізків дотичних від цієї точки до точки дотику рівні;
b) пряма, що проходить через центр кола і цю точку, ділить кут між дотичними навпіл.

Коло та круг.

Сьогодні на уроці ви ознайомитеся з поняттям «коло», «круг», їх елементами, навчитеся зображувати   коло і круг та  знаходити на рисунках елементи кола, давати означення кола, круга та їх елементів.

Запам'ятайте основні поняття.

Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки – центра кола.

Радіус кола – відстань від точок кола до його центра. 

Хорда – відрізок, який з'єднує будь-які дві точки кола. 

Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола.

Дотична – пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. 

Виконайте завдання:

1. Накресліть коло з центром в точці О. Проведіть радіус, діаметр та хорду.  

Назвіть їх великими латинськими літерами та запишіть в зошит.

                                                                 

2. Радіус кола дорівнює 7 см. Чому дорівнює діаметр цього кола?

3. Діаметр кола дорівнює 25 см. Чому дорівнює радіус?