Тема 6.Системи лінійних рівнянь з двома змінними.

Лінійне рівняння з двома змінними.

 Рівняння виду 

ax+by=c, де a,b,c — числа (коефіцієнти), x та y - змінні, називається лінійним рівнянням з двома змінними .

Розв'язком рівняння ax+by=c називають будь-яку пару чисел (x;y), яка задовольняє це рівняння, тобто перетворює рівність зі змінними ax+by=c на правильну числову рівність.

Приклад:

 

Зобразити розв'язок лінійного рівняння з двома змінними x+y=3 точками у координатній площині xOy.

 

Підберемо кілька розв'язків заданого рівняння, тобто кілька пар чисел, які задовольняють рівняння: (3,0),(2;1),(1,2),(0,3),(4;−1).

 

Побудуємо у координатній площині xOy ці точки. Усі вони лежать на одній прямій t.

 

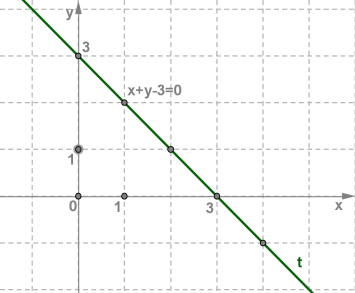
Пряма t є графіком рівняння x+y=3, або пряма t є геометричною моделлю цього рівняння.

 

Отже, якщо пара чисел (x; y) задовольняє рівняння ax+by=c , то точка 

М(x;y) належить прямій t.

І навпаки, якщо точка М(x;y) належить прямій t, то пара чисел (x;y) задовольняє рівняння ax+by=c.

 

Справедливою є така теорема:

Якщо хоча б один з коефіцієнтів a,b лінійного рівняння ax+by=c відмінний від нуля, то графіком рівняння служить пряма лінія.

  

Алгоритм побудови графіка рівняння ax+by=c, де a≠0,b≠0

 

1. Надати змінній x конкретне значення x=x1; з рівняння 

ax1+by=c знайти відповідне значення y=y1.

2. Надати змінній x інше значення x=x2;

з рівняння ax2+by=c знайти відповідне значення y=y2.

3. Побудувати на координатній площині xOy точки: (x1;y1)(x2;y2)

4. Провести через ці дві точки пряму — вона і буде графіком рівняння

ax+by=c

 

Приклад:

Побудувати графік рівняння x−2y−4=0.

Будемо діяти за алгоритмом.
1. Нехай x=0, тоді отримаємо:

 

0−2y−4=0,−2y=4,y=4:(−2)y=−2

 

2. Нехай y=0, тоді отримаємо:

x−2⋅0−4=0x−4=0x=4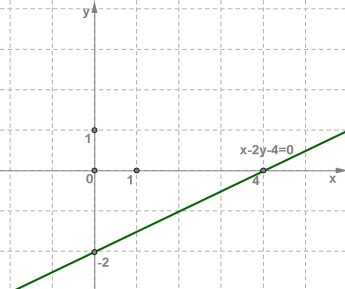

 

3. Побудуємо на координатній площині xOy отримані точки:

(0;−2) та (4;0)

 

4. Проведемо через ці точки пряму.

 

 

 

Вона і буде графіком лінійного рівняння x−2y−4=0.

Системи двох лінійних рівнянь із двома змінними

Теорія:

Маємо два лінійних рівняння з двома змінними x та y:

 

a1x+b1y+c1=0 і a2x+b2y+c2=0.

 

Треба знайти такі значення змінних x і y,  які водночас задовольняли б і перше, і друге рівняння, тобто перетворювали кожне з рівнянь у правильну рівність. Інакше кажучи: треба знайти спільний розв'язок обох рівнянь (x;y), або розв'язати систему даних рівнянь.

Зверни увагу!

Рівняння системи записують одне під одним і об'єднують спеціальним символом — фігурною дужкою:

{a1x+b1y+c1=0,a2x+b2y+c2=0.

Пара значень (x;y), яка одночасно є розв'язком і першого, і другого рівнянь системи, називають розв'язком системи.

Розв'язати систему — це означає знайти всі її розв'язки або встановити, що їх немає.

Завдання 1. Розв'язати систему рівнянь

 

{x+2y−5=0,2x+4y+3=0.

 

Графіком рівняння x+2y−5=0 є пряма.
Знайдемо дві пари значень змінних x та y, що задовольняють цьому рівнянню.

x	5	0
y	0	2,5

Побудуємо на координатній площині xОy пряму l1, яка проходить через ці дві точки.

 

Графіком рівняння 2x+4y+3=0 також є пряма.
Знайдемо дві пари значень змінних x та y, що задовольняють цьому рівнянню.

x	−1,5	2,5
y	0	−2

 

Побудуємо на координатній площині xОy пряму l2, що проходить через ці дві точки.

 

 

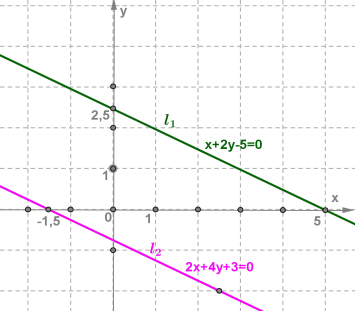
Прямі l1 і l2 паралельні. Отже, система не має розв'язків, оскільки немає точок, що задовольняють одночасно і першому, і другому рівнянню, тобто належать одночасно і першій, і другій із побудованих прямих.
 

Відповідь: система не має розв'язків.

 

Завдання 2. Розв'язати систему рівнянь:

 

{2x−y−5=0,2x+y−7=0.

 

Побудуємо графіки рівнянь системи, приведемо кожне рівняння до вигляду лінійної функції. Отримаємо з першого рівняння y=2x−5 і з другого рівняння y=−2x+7.

 

Графіком рівняння y=2x−5 є пряма.

 

Знайдемо дві пари значень змінних x та y, що задовольняють цьому рівнянню.

x	0	3
y	−5	1

 

Побудуємо на координатній площині xОy пряму l1, яка проходить через ці дві точки.
Графіком рівняння y=−2x+7 також є пряма.

 

Знайдемо дві пари значень змінних x та y, що задовільняють цьому рівнянню.

 

x	0	1
y	7	5

 

Побудуємо на координатній площині xОy пряму l2, що проходить через ці дві точки.

 

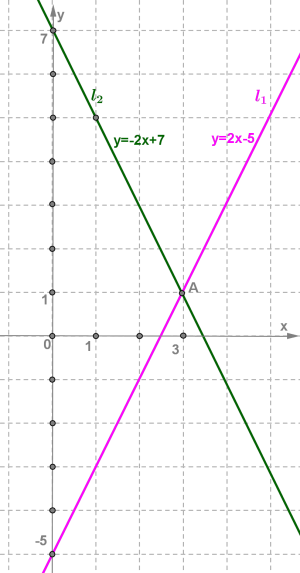
Прямі l1 і l2 перетинаються в точці A, координати якої — єдиний розв'язок даної системи. 

Відповідь: (3;1).

 

Для розв'язання цих двох прикладів застосовувався графічний метод розв'язання системи лінійних рівнянь.

  

Але цей метод є наближеним, оскільки координати точки перетину за кресленням не завжди легко визначити. Але все-таки графічний метод розв'язання системи лінійних рівнянь дуже важливий, коли необхідно визначити кількість розв'язків.