А 8 Тема 2. Квадратні корені. Дійсні числа

 

 Функція обернена пропорційність, її графік і властивості

Функція y=kx

Познайомимося з новою функцією: y=kx

 

Коефіцієнт k може приймати будь-які значення, крім k=0. Розглянемо спочатку випадок, коли k=1; отже, спочатку поговоримо про функцію y=1x.

 

Щоб побудувати графік функції y=1x, надамо незалежній змінній x декілька конкретних значень та обчислимо (за формулою y=1x) відповідні значення залежної змінної y.

 

Щоправда, в цьому випадку зручніше здійснювати обчислення та побудову поступово — спочатку надавати аргументу лише додатних значень, а потім — лише від'ємних. 

Якщо x=1, то y=1 (нагадаємо, що ми користуємося формулою y=1x);

Підбираючи значення, ми склали наступну таблицю:

 

x	1	2	4	8	12	14	18
y	1	12	14	18	2	4	8

 

Побудуємо знайдені точки на координатній площині xOy.

Далі

якщо x=−1, то y=−1;і тд.

ми склали наступну таблицю:

 

x	−1	−2	−4	−8	−12	−14	−18
y	−1	−12	−14	−18	−2	−4	−8

 

Побудуємо знайдені точки на координатній площині xOy.

 

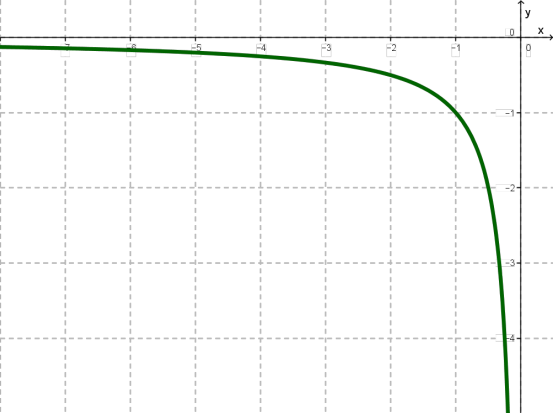
Тепер об'єднаємо два етапи в один, тобто із двох малюнків зробимо один.

 

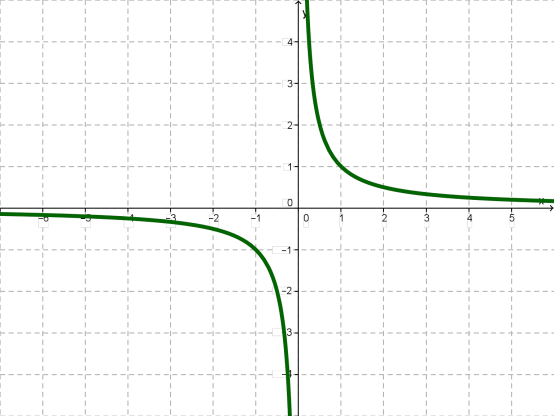
Це і є графіком функції y=1x, який називається гіперболою.

Властивості:

• область визначення функції складається з усіх чисел, крім 0;

• область значень функції складається з усіх чисел, крім 0

• графік функції називається гіпербола, вітки якої розміщені в І і ІІІ,

•      координатних чвертях, якщо > 0, і в ІІ та ІV, якщо < 0.

•      вітки гіперболи необмежено наближаються до осей координат.

•