Г 9 Тема 4. ПРАВИЛЬНІ МНОГОКУТНИКИ. ДОВЖИНА КОЛА. ПЛОЩА КРУГА

Площа круга та його частин

Довжина кола і дуги кола.

Для всіх кіл правильним є те, що відношення довжини кола до його діаметра є одним і тим самим числом.

Це число прийнято позначати грецькою буквою π («пі»). У цього числа за комою міститься нескінченна безліч цифр, порядок яких не повторюється. У наш час, коли обчислювальні технології дуже розвинені, можна обчислити багато значущих цифр. Скільки цифр використовувати в розрахунках, потрібно вирішувати залежно від того, яка точність необхідна. Іноді використовується навіть округлення до цілих 

π≈3, але найчастіше використовується π≈3,14.

 

Цікаво, що в березні (3 місяць) 14-го числа у світі неофіційно відзначають день π, до якого приурочують математичні конкурси та інші цікаві події.

Довжина кола позначається через C, діаметр і радіус D=2R, отже:

 

C=π⋅D  або  C=2π⋅R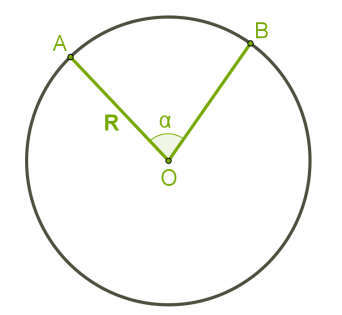

 

Оскільки довжина всього кола дорівнює C=2π⋅R, то довжина дуги величиною 1° дорівнює:

 

2πR360°=πR180°

 

Якщо градусна міра дуги дорівнює α градусам, то довжина такої дуги ∪AB=l  виражається формулою l=πR180°⋅α.

Правильні многокутники та кола.

Кількість сторін правильного n-кутника	n = 3	n = 4	n = 6
Сторона правильного n-кутника	а 3 = R	а 4 = R	а 6 = R
	а 3 = 2r	а 4 = 2r	а 6=

           

Кількість сторін правильного n-кутника	n = 3	n = 4	n = 6
Радіус описаного кола	R 3 =	R 4 =	R 6 = а
Радіус вписаного кола	r 3 =	r 4 =	r 6 =

ПРАВИЛЬНІ МНОГОКУТНИКИ ТА ЇХ ВЛАСТИВОСТІ.

 Сьогодні на уроці ви познайомитеся з поняттям правильного многокутника, центрального кута правильного многокутника, радіуса описаного та вписаного кіл.

Опуклий многокутник називається правильним, якщо всі його сторони рівні і всі кути рівні.

Рівносторонній трикутник і квадрат — приклади правильних многокутників. На малюнку зображено правильний п’ятикутник і правильний шестикутник.

        Якщо правильний многокутник має n сторін, то сума всіх його кутів (внутрішніх) дорівнює 180°(п - 2), а один з них — у n разів менший, тобто дорівнює

.

Чим більше число n, тим більший кут правильного n-кутника.

ТЕОРЕМА 11

Якщо многокутник правильний, то навколо нього можна описати коло і в нього можна вписати коло.  

Центром кола, вписаного в правильний многокутник, і кола, описаного навколо нього, є одна й та сама точка О. Її називають центром правильного многокутника.

Кут, під яким з центра правильного многокутника видно його сторону, називають центральним кутом многокутника. Перпендикуляр, опущений з центра правильного многокутника на його сторону, — апофема правильного многокутника.  Міра центрального кута правильного n-кутника дорівнює . 

У вершинах правильних многокутників звичайно знаходяться центри кульок у підшипниках, центри отворів на фланцях, кінці зубів круглих пилок (мал. ) тощо.

Плитки і плити для покриття підлоги в будинках, площ і вулиць, аеродромів здебільшого виготовляють у формі правильних многокутників.

            

Перегляньте відео:

Запитання і завдання для самоконтролю

1. Сформулюйте означення правильного многокутника.

2. Як інакше називають правильний трикутник? А правильний чотирикутник?

3. Чому дорівнює сума кутів правильного многокутника?

4. Чому дорівнює міра внутрішнього кута правильного n-кутника?

5. Чому дорівнює міра центрального кута правильного n-кутника?

6. Чи можна навколо кожного правильного многокутника описати коло?

7. Чи можна у кожний правильний многокутник вписати коло?

8. Що називають центром правильного многокутника?

9. Що називають апофемою правильного многокутника?