07.10
Додавання і віднімання дробів з різними знаменниками
Щоб додати або відняти дроби, знаменниками яких є різні многочлени, необхідно:
Якщо знаменниками дробів є многочлени, то спільним знаменником цих дробів також буде многочлен, який знаходимо наступним чином:
- знаменники всіх дробів розкладаються на множники (якщо це необхідно та можливо);
- з одного знаменника беруться всі множники, а з інших тільки ті, яких немає в першому знаменнику (тобто ті, яких «бракує»).
Якщо многочлени в знаменниках дробів неможливо розкласти на множники, то спільний знаменник таких дробів дорівнює добутку знаменників усіх дробів.
Аби безпомилково визначити додатковий множник для кожного дробу, отриманий спільний знаменник краще одразу записати в знаменнику «нового» дробу.
Аби безпомилково визначити додатковий множник для кожного дробу, отриманий спільний знаменник краще одразу записати в знаменнику «нового» дробу.
Завдання: №93,95,97
21.05.-25.05. Контрольна робота з теми "Квадратні рівняння "
18.05.-20.05.Розвязування задач за допомогою квчадратних рівнянь.
Параграф 3, п.25. № 828,830,834
12.05.-15.05.Рівняння, які зводяться до квадратних. Біквадратні рівняння.
Тема: Конференція Zoom. Біквадратні рівняння.
Время: 13 травня 2020 12:00
Идентификатор конференции: 323 692 8986
Пароль: 6LCSUR
Завдання. № 803, 813

Конференція Zoom Тетяна Садовенко
Время: 5 травня 2020 12:00
Ідентифікатор конференції: 733 3501 5058
Завдання:параграф 3, п.24. № 797, 799, 801.
27.04.-30.04.Квадратний тричлен
завдання:ст.182-184. № 775,778,780, 783
16.04.-24.04. Теорема Вієта.
завдання: №736, 737

07.04. - 15.04.
Самостійна робота
Домашнє завдання: № 706, 715 ( Підказка: Ці рівняння спочатку потрібно звести до квадратних, а потім розв"язати) - чекаю у VIBER
З0.03.- 07.04.
Формули коренів квадратного рівняння
Опрацювати параграф 3.п.21. № 702, 703,704, 711
Про неповні квадратні рівняння (відео)
Неповні квадратні рівняння
Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо
 , то , то  перетворюється у лінійне рівняння перетворюється у лінійне рівняння 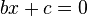 . Якщо хоч один коефіцієнт . Якщо хоч один коефіцієнт  або або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів: дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:
Розв'язування неповних квадратних рівнянь
Приклад. Розв’яжіть рівняння:

Розв’язання.
|
 ;
; 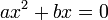 ;
; 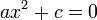 .
.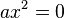 рівносильне рівнянню
рівносильне рівнянню  і тому завжди має тільки один корінь
і тому завжди має тільки один корінь  .
.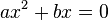 розв'язується винесенням за дужки
розв'язується винесенням за дужки  :
:  . Таке рівняння має два корені:
. Таке рівняння має два корені: 
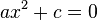 рівносильне рівнянню
рівносильне рівнянню  . Якщо
. Якщо  , воно має два дійсних розв'язки, якщо
, воно має два дійсних розв'язки, якщо 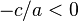 — жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то
— жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то 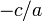 - додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число
- додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число
Немає коментарів:
Дописати коментар